・k近傍法ってなに？
・k近傍法を直感的に理解したい......
と悩んではいませんか？
本記事では、k近傍法の仕組みや数式、Pythonでの実装やメリット・デメリットまで、データサイエンスを大学で学んでいるしょーが解説していきます。
k近傍法は対象の点から近い点のクラスで判断する分類手法です！
本記事の信頼性
こんな悩みがある方読んで欲しい
- k近傍法の仕組みが知りたい
- k近傍法って何で使えるの？
- Pythonで実装したいけどどうやってやるの？
- k近傍法を使うメリット・デメリットってなに？
それでは本編です！
月額980円で学べる！
データサイエンスを学べるスク―ルって全部高くない？
確かに、データサイエンスのスクールは数十万円かかるものばかりで、うんざりですよね。
そんなあなたにおすすめなのが、たった月額980円で学べる『スタアカ』です！
もうデータサイエンスを学ぶために高額なお金を払う必要はありません。
サブスクなのでいつでも解約OK。手軽に始めてみませんか？
＼月額980円／
講座が毎月追加されるので今後値上がりする可能性大、今が買いどき！
k近傍法の概要
k近傍法とはあるデータを分類したい時に用いる手法です。
分類したいデータがあるけど1つ1つ振り分けるのは面倒ですよね。
k近傍法では事前にクラス分けしたデータを使うことで、分類したいデータを自動的に分類します。
仕組みがシンプルで理解しやすい手法です。
k近傍法：k個の隣接点から分類予測を行う手法
k近傍法(k-nearest neighbor)は最も近いk個の隣接点を参考にして予測を行う教師あり学習です。
既にクラス分けされたデータを学習しておき、そのデータの中で分類したいデータ点に最も近いk個の隣接点を取り出し、最も個数の多いクラスに対象のデータ点を分類します。
例を用いてかみ砕いて説明していきます！
上記のような例の場合、あなたは対象のデータ点がどのクラスタに属すると思いますか？
赤色のクラスタかな？
あなたは一番近い隣接点が赤色の点だと思って、赤色と答えましたね。
この状態をk=1で判断していると言います。
k近傍法では図のように分類したいデータ点を中心に円を拡げ、近くにある点(近傍点)を探します。
表に表すと以下の通りです。
| 色 | 円の中にある点の数 |
|---|---|
| 赤 | 1 |
| 緑 | 0 |
| 紫 | 0 |
では次のような場合はどうでしょうか？
2つ目の例では、k=18、円の中に18個まで点を入れてよいとしました。
各データ点の個数を表に表してみましょう。
| 色 | 円の中にある点の数 |
|---|---|
| 赤 | 8 |
| 緑 | 9 |
| 紫 | 1 |
円の中にある点の数がもっとも多いのが緑に変わりました。
k近傍法は分類したい点に近いk個の点を調べて、それぞれのクラスの点の数を比較して1番多いクラスに属すると決める手法です。
k近傍法について直感的に理解できたところで、実用例について見ていきましょう。
k近傍法が使える場面
k近傍法はシンプルな分類手法のため、多くの場面で活用されています。
例として以下の3つをご紹介します。
- 手書きの文字認識
- 異常の検知
- 情報の推薦システム
工場で活用できるものから、あなたの身近な所まで分類手法が用いられています。
それぞれ解説していきます。
1. 手書きの文字認識
手書きの文字認識にk近傍法を使えます。
手書きの文字認識は、iPadの手書き文字のテキスト変換で用いられているほど身近で実用的な機能です。
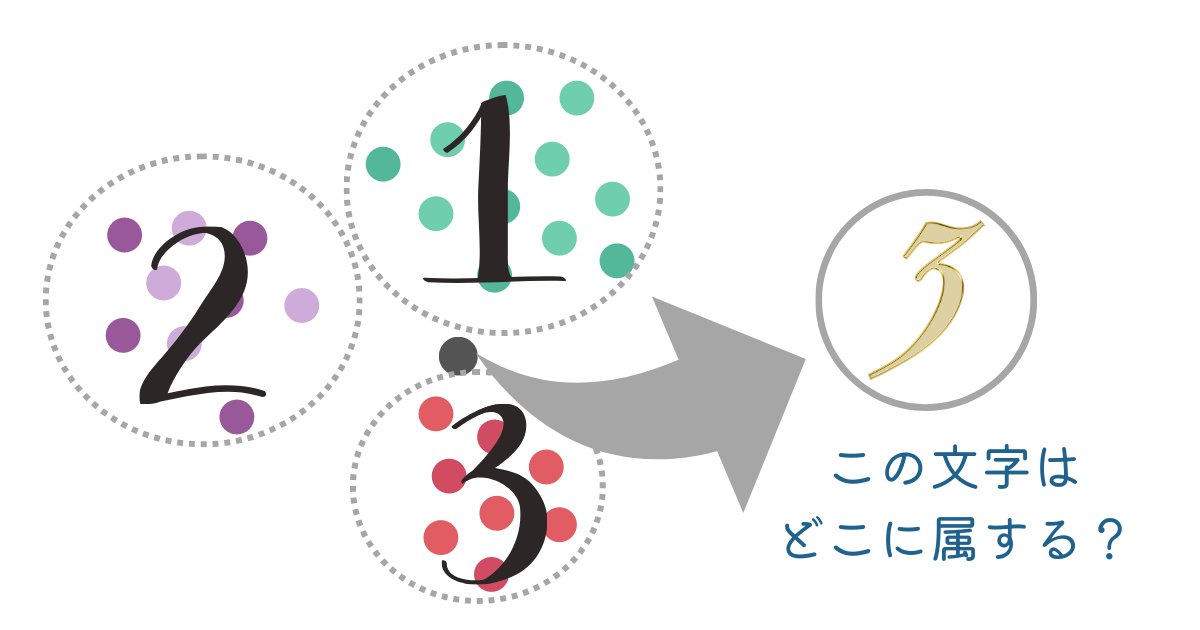
1,2,3の手書き文字を画像認識で数値化し散布図に表し、それぞれクラスタに分かれたと仮定します。
このような場合にグレーの点の文字がどの文字になるかを判断するのがk近傍法です。
2. 異常の検知
k近傍法は正常値と異常値の分類と捉えると、異常検知にも応用できます。
工場では日々多くの製品が製造されており、正常値の製品と異常値の製品のデータが蓄積されています。そのデータを活用することで異常を自動検知できるのです。
グラフで表してみましょう。
ある工場でセンサーを用いて製品を検査したところ、グレーの点に位置しました。この点は正常値か異常値か、どちらでしょうか？
青が正常値、赤が異常値の集合である場合、あなたは赤（異常値）であると判断するでしょう。
このように数値で表せればk近傍法を用いて自動で異常検知を行えます。
3. 情報の推薦システム
amazonやECサイトで用いられている情報推薦システムにもk近傍法を適用できます。
商品ごとにクラスタを分類したりユーザーごとにクラスタを分類したりすることでもっとも近いk個の点を参考にできるのです。
ただし、あくまで適用できるだけであるため、現在多くのECサイトでは独自のアルゴリズムや複雑なアルゴリズムが採用されている場合が多いでしょう。
直感的理解と具体例が分かったところで数式で理解してみましょう！
k近傍法で使われている距離の公式
k近傍法では距離の公式を用いて近くの点との距離を求めます。
今回はユークリッド距離という直線的な距離を求める公式で考えましょう。
式では以下のように表せます。
$$d(A, B) = \sqrt{(c - a)^2 + (d - b)^2}$$
数式だけでなく図解でも見てみましょう。
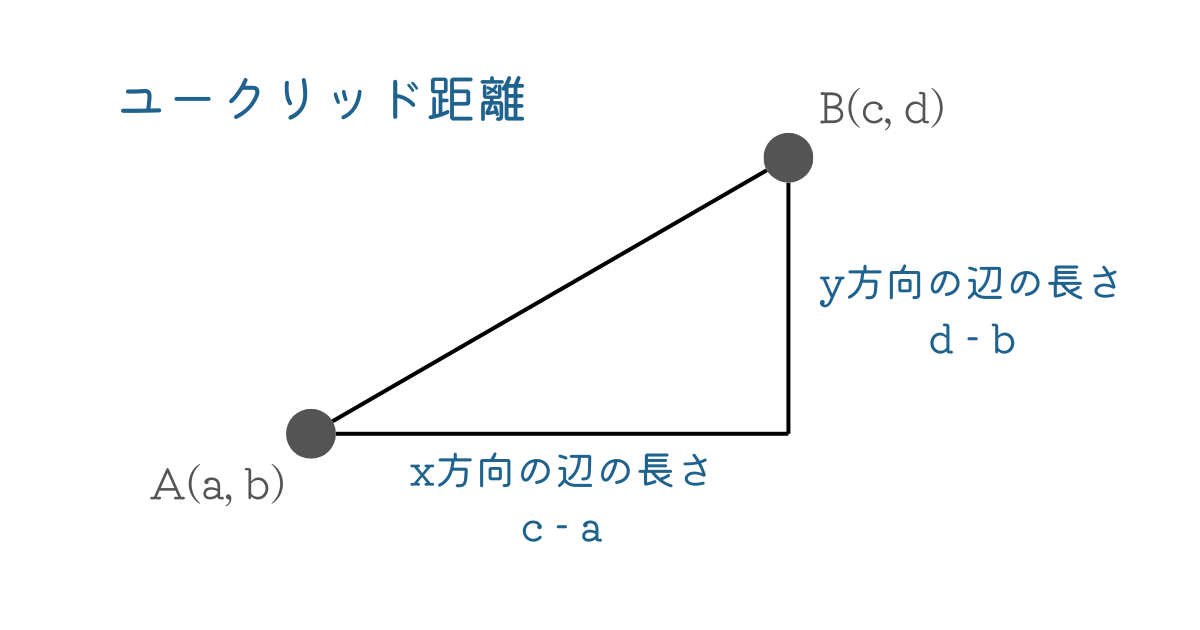
ユークリッド距離は三平方の定理の定理を用いて解けます。
三平方の定理が分からない人はユークリッド距離の公式を暗記でOKです！
k近傍法の手順
k近傍法の概要について理解できたところで手順を追って実践してみましょう。
Pythonのコードも併せて記載しているので、分析したいデータがある場合は修正して使用してください。
STEP1. 必要なライブラリをインポート
まず、Pythonで実装するために必要なライブラリをインポートしましょう。
先ほどまで紹介していたk近傍法のアルゴリズムは関数で実行できます。
関数を実行するためのライブラリを読み込む必要があります。
# 必要なライブラリのインポート
# k近傍法のアルゴリズムのライブラリ
from sklearn.neighbors import KNeighborsClassifier
# 訓練データとテストデータに分割するライブラリ
from sklearn.model_selection import train_test_split
# k近傍法の評価のためのライブラリ
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
# データセットを読み込むためのライブラリ(今回はアヤメの分類)
from sklearn.datasets import load_irisSTEP2. データの準備と訓練データ、テストデータへの分割
次に、実際に分析したいデータを読み込み、データを訓練用とテスト用に分割しましょう。
今回は機械学習の分野で良く用いられているアヤメのデータで分析を進めます。
print関数でデータの確認をすることを忘れずに行いましょう。
# データの準備
iris = load_iris()
print(iris)データの準備ができたらデータを分割しましょう。
訓練データとテストデータで分けることでデータの学習と評価ができます。
- 訓練データ：k近傍法の学習に使うデータ
- テストデータ：手法がどれだけ正しいのか評価するために使うデータ
関数内の変数は以下のような意味です。
- test_size=0.2 : テストデータに2割のデータを配分
- random_state=1 : 出力を同じにするため
# データセットをトレーニングセットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)STEP3. 距離の計算方法の選択
データ間の距離を測るために距離の計算方法を変数で設定しましょう。
今回はユークリッド距離を距離の公式として採用します。
# 距離の計算方法の設定
# 通常はデフォルトのユークリッド距離が使用されますが、必要に応じて他の距離尺度を指定することも可能です
distance_metric = "euclidean" # ユークリッド距離STEP4. kの値の選択
何個の近傍点から判断するのかを決めるため、kの値を設定しましょう。
今回は自分で設定していますが、最適なkを見つけ出すこともできます。
# kの値の選択
k = 10 # 予測に使う近傍点の個数STEP5. k近傍法による予測を実行
いよいよk近傍法を実行します。
先ほどまでで設定した変数を引数で指定して、モデルを学習させていきます。
そして、学習させたモデルでテストデータのデータから正解を予測する流れです。
# k近傍法モデルの作成と訓練
# k近傍法のやり方を指定
knn = KNeighborsClassifier(n_neighbors=k, metric=distance_metric)
# 訓練データで学習
knn.fit(X_train, y_train)
# テストデータの予測
y_pred = knn.predict(X_test)STEP6. 評価指標を用いて評価する
テストデータの正解と先ほど予測したデータを比較することで評価します。
k近傍法の評価指標としてよく用いられる正解率や適合率、再現率、F値を評価指標としました。
今回は3つのクラスの分類であるため、各指標ごとの計算で平均を取るマクロ平均の形です。
# k近傍法の評価
# 第3引数でマクロ平均を指定(各指標を計算してから平均を取る)
print("正解率: {:0.3f}".format(accuracy_score(y_test, y_pred)))
print("適合率: {:0.3f}".format(precision_score(y_test, y_pred, average="macro")))
print("再現率: {:0.3f}".format(recall_score(y_test, y_pred, average="macro")))
print("F1: {:0.3f}".format(f1_score(y_test, y_pred, average="macro")))評価指標について詳しく知りたい方は『評価指標』の記事をご参照ください。
k近傍法のメリットとデメリット
k近傍法のメリット
k近傍法を用いるメリットは以下の3つです。
- シンプルなアルゴリズムのため理解しやすい
- Pythonでの実装が容易
- 非線形や複雑なデータにも適用しやすい
k近傍法は機械学習の手法の中でもシンプルで理解しやすいです。
また、Pythonでの実装も容易であることから業務にも使用しやすいでしょう。
さらに、k近傍法は非線形な関係や複雑なデータにも適用できる柔軟性も持ち合わせています。
k近傍法のデメリット
k近傍法のデメリットは以下の3つです。
- 計算コストがかかる
- 特徴量に対して前処理を加える必要がある
- kの設定が難しい
k近傍法は、それぞれの点との距離を毎回計算するため、計算コストが非常に高いです。
また、身長と体重といったそれぞれで単位が違うものは大きさを揃えなくてはなりません。
さらに、kを小さく設定してしまうと過剰にデータに適合してしまう（過学習）ことがあることも注意しましょう。
過学習について詳しく知りたい方は『過学習（Overfitting）とは？起こる原因から見分け方・対策方法までわかりやすく解説！』の記事をご参照ください。
まとめ
k近傍法は分類する時に使う手法で、シンプルで実用的です。
分類するための手法であることから、日常や業務への実装も容易に行えます。
記事内では、文字認識や異常検知、情報推薦システムへの応用例を紹介しました。
さまざまな場面で実装できるので、身近なデータから分類してみましょう。
「機械学習の勉強がなかなか上手く進まない...」
「勉強しても全体像が見えてこない...」
「本当にデータサイエンティストになれるのかな...」
と不安に感じてはいませんか？
僕も勉強しながら同じような悩みを常に持っていました。
ですが、そんな僕の悩みをまるっと解決してくれるサービスをついに見つけました。
データサイエンスを学べるサービスなんて高額でしょ？
データサイエンスを学ぶために高額なお金を払う必要はありません。
僕が利用している『スタアカ』のライトプランは月額980円で動画見放題のコスパ最強サブスクです。
たった月1000円で、もう二度と独学で悩まずに済みます。
正直、「就職・転職までサポートしてほしい」という方にはおすすめできません。
ですが、「勉強の道しるべが欲しい！」「学習を効率的に進めたい」という方にはこの上ないサブスクです。
データサイエンスを学びたい方に最強のサブスク『スタアカ』を気軽に始めてみませんか？
＼月額たった980円！／
講座が毎月追加されるので今後値上がりする可能性大、今が買いどき！
