- k-means法ってなに？
- どんなアルゴリズムなの？
とお悩みではないですか？
本記事では、k-means法が使える場面やアルゴリズム、欠点、そしてPythonでの実装について解説していきます。
k-means法はデータをグループに分けるクラスタリングの手法です。
データのグループ分けは顧客分析などビジネスで役立つため、k-means法の汎用性は高まっています。
本記事の信頼性
こんな悩みがある方読んで欲しい
- k-means法ってなに？
- k-means法の使える場面とは？
- アルゴリズムが分からない
- 欠点ってあるの？
それでは本編です！
月額980円で学べる！
データサイエンスを学べるスク―ルって全部高くない？
確かに、データサイエンスのスクールは数十万円かかるものばかりで、うんざりですよね。
そんなあなたにおすすめなのが、たった月額980円で学べる『スタアカ』です！
もうデータサイエンスを学ぶために高額なお金を払う必要はありません。
サブスクなのでいつでも解約OK。手軽に始めてみませんか？
＼月額980円／
講座が毎月追加されるので今後値上がりする可能性大、今が買いどき！
k-means法（k平均法）とは
k-means法（k平均法）とは、データをクラスタというグループに分けるための手法のことです。
データをクラスタに分けることをクラスタリングと言い、k-means法を用いることでクラスタリングが行えます。
k-means法は教師なし学習に分類され、データに事前にラベル付けをしておく必要がありません。
そのため、手元にあるデータをすぐにk-means法で分けたいクラスタ数にクラスタリングできます。
クラスタリングはビジネスで顧客のグループ分けなどに用いられており、k-means法を使えるようになれば、ビジネスシーンでも活用できます。
以下でk-means法が使える場面について解説していきます
k-means法が使える3つの場面・活用例
k-means法は、データをクラスタに分けるクラスタリングの手法であることから、様々な場面で活用されています。
ここでは、主に以下の3つを挙げます。
- 顧客のグループ分け
- 文書や情報の分類
- 社会ネットワークの分析
それぞれ多くの場面で用いられている例です。
それぞれ解説していきます。
顧客のグループ分け
顧客のグループ分けにk-means法が用いられます。
ビジネスでは、どの顧客に商品を販売するのかというターゲットの決定が重要になります。
また、現在発売している商品がどのような顧客層にハマっているのかを分析することも重要です。
なので、顧客層の分析のために顧客のグループ分け（グルーピング）を行う必要があります。
手元にあるデータからすぐにクラスタリングを行えるため、ビジネスでもk-means法は活用できます。
例えば、ある会社が顧客データを持っていて、購買履歴や顧客の属性を記録しているとします。
k-means法を用いることで、顧客を購買傾向や興味によってグループ分けできます。
k-means法で得た情報は、キャンペーンのターゲット設定や商品の方向性の変更の判断材料になります。
このように、顧客をグループ分けできるk-means法はビジネスに直結するのです。
文書や情報の分類
文書や情報の分類にもk-means法を活用できます。
文書や情報の分類は多くの場面で用いられています。
例えば、Netflixなどの動画配信サービスであなたへのおすすめが表示されますよね。
おすすめをするためには、似ているユーザーを特定するかあなたの見ている動画と似た種類の動画を見つけなければなりません。
さまざまな動画の属性をデータにしてk-means法を行うことで、動画をグループ分けでき、似た動画をユーザーに提示できるのです。
また、ニュースサイトの記事の分類やレビューや感想をポジティブ・ネガティブに分類する際に活用されています。
社会ネットワークの分析
社会ネットワークの分析もk-means法で行えます。
社会ネットワークとは人同士の社会的なつながりや関係性を示したもので、現代社会では社会ネットワークが多く存在します。
社会ネットワーク分析を行うことで、特定のコミュニティや影響力のある人物を特定できます。
ビジネスにおいては、社会ネットワーク分析を行うことで、自社の商品のターゲット層を決定でき、より効率的なプロモーション戦略を打ち出せるのです。
そのため、k-means法は社会ネットワーク分析の需要の高さから重宝される手法になります。
次にk-means法のアルゴリズムについて解説していきます
k-means法の手順・アルゴリズム
k-means法は機械学習手法の中でも分かりやすいアルゴリズムです。
k-means法の手順は以下の4ステップになります。
- クラスタ数を決定・適当に重心を設定する
- 各データ点で重心との距離を計算し、クラスタに分ける
- 重心点を計算し直す
- 重心点の変動がなくなるまで繰り返す
k-means法は重心点を決めて、距離を計算して修正していくことでクラスタリングを行います。
それぞれのステップについて解説していきます。
STEP1. クラスタ数を決定・適当に重心を設定する
まずクラスタ数を決めます。
クラスタ数とはデータを分けるグループの数のことです。
事前に何個のグループに分けるかを決めている場合はそのグループ数にしましょう。
クラスタ数を決定したら、初期の値として適当に重心を設定します。
例えば、以下のような散布図のデータでk-means法を進めてみましょう。
今回はクラスタ数を3つとします。
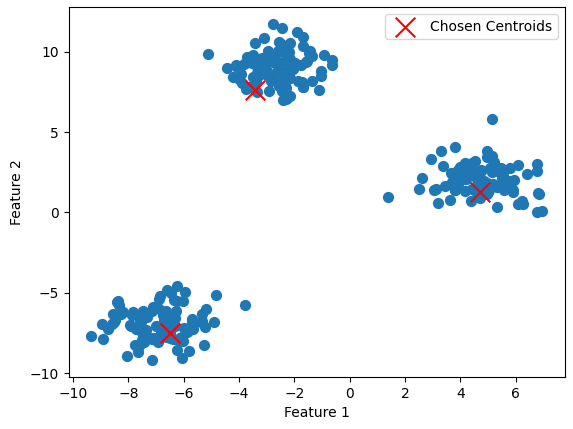
上の画像の×が適当に決めた重心です。
重心の初期値を定めたら、次のステップに移りましょう。
STEP2. 各データ点で重心との距離を計算し、クラスタに分ける
次に定めた重心の初期値と各データ点との距離を計算し、クラスタに分けます。
今回はクラスタ数を3つとしたため、3つの重心と各データ点との距離となります。
先ほど示した散布図で重心と線で結んでみましょう。
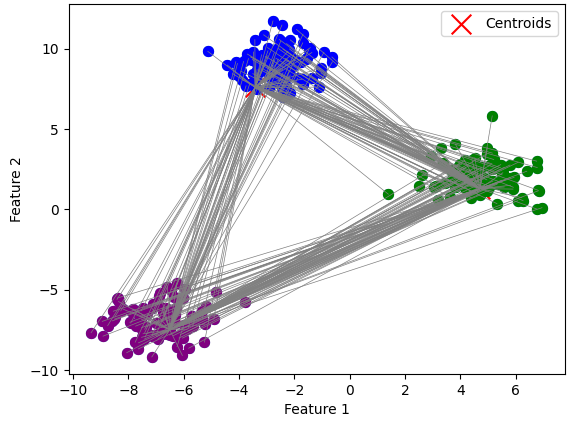
すべての点と重心との距離が計算することで、対象の点と最も距離が短い重心のクラスタに点が属すると判断できます。
実際、上の画像のように青・緑・紫とクラスタに分けられます。
このように、クラスタに分けられたら次のステップです
STEP3. 重心点を計算し直す
重心の初期値はあくまで適当に決めたものであるため正確な重心ではありません。
そのため、重心点を再度計算し直さなければならないのです。
重心点の計算は、重心があるクラスタのすべてのデータ点から算出します。
そして算出された重心を次の重心にして、1回の重心の更新が終了になります。
STEP4. 重心点の変動がなくなるまで繰り返す
STEP3までで一回の重心の更新を行いました。
しかし、重心を更新して距離を計算し直すとデータ点によっては所属するクラスタが変わることがあります。
そのため、、データ点の変化に伴って、もう一度重心を更新しなくてはならないのです。
このように、重心を更新する作業（STEP2とSTEP3）を繰り返して、重心点の変動がなくなるまで続けます。
その結果、正確な重心を求めることができ、クラスタリングが終了するのです。
以下が実際に重心点の変動がなくなった散布図になります。
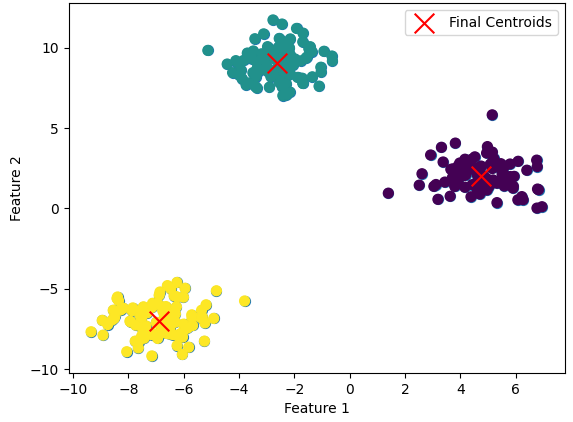
このようなクラスタリングをk-means法を用いて行えます。
例えば、今回の散布図が顧客属性のデータであったとします。
3つのクラスタに分けることで、どの顧客が似たような商品を買っているのかを分析できますね。
その結果、特定の顧客層に対してアプローチするように戦略を立案することも可能です。
このように、k-means法の結果はビジネスにおいて重要な決定の判断材料になります。
k-means法の3つの欠点
アルゴリズムが簡単で理解しやすいk-means法ですが、3つの欠点があります。
代表的な欠点は以下の3つです。
- クラスタ数を事前に決める必要がある
- 重心の初期値によって結果が変わる
- 外れ値やノイズの影響を受けやすい
k-means法を行ううえで欠点を理解しておくと、結果を正しく解釈できます。
なので、必ず抑えておくようにしましょう。
それぞれ解説していきます。
クラスタ数を事前に決める必要がある
k-means法は、最初にクラスタ数を決めなくてはならないのが欠点です。
事前に分けたいクラスタ数が決まっている場合は良いですが、それぞれのデータには最適なクラスタ数が存在します。
もし、とりあえずデータをクラスタリングして特徴を見出したいという場合には、最適なクラスタ数に分けなくてはなりません。
そのため、実務ではクラスタ数を変化させて繰り返しk-means法を行って重心とデータ点との誤差を見るエルボー法を用います。
エルボー法によって、クラスタ数の変化に対する誤差の変化の大きさを可視化し、最も変化が大きくなったところを最適なクラスタ数とします。
クラスタ数を多くするほど、必ず誤差は減少していくため、最も変化が大きくなったところを最適なクラスタ数とするのです。
最適なクラスタ数を把握するために何回もk-means法を行う必要があるのが欠点となります。
もし、クラスタ数が決まないでクラスタリングを行いたい場合は、DBSCANという手法がおすすめです。
DBSCANについて詳しく知りたい方は『DBSCANとは？アルゴリズムやメリット、Pythonコードまで解説』の記事をご参照ください。
重心の初期値によって結果が変わる
重心の初期値の設定（STEP1）によって、クラスタリングの結果が大きく変わってしまいます。
初期値から距離を計算して1回目のクラスタリングを行いますよね。
その結果をもとに重心を更新するため、1回目のクラスタリングも重要なのです。
そのため、初期値どうしが良くない位置関係にある場合、クラスタリングの結果が悪くなる可能性があります。
例えば、重心の初期値を極端な値（外れ値）に設定してしまうと、各データ点との距離が離れすぎていて、値が1つだけのクラスタになってしまいます。
そのため、重心の初期値を変えて、複数回k-means法を実行することをおすすめします。
また、必ずクラスタリングの結果を色付けして散布図で確認し、おかしくないかを判断してください。
外れ値やノイズの影響を受けやすい
重心の初期値でも外れ値について述べましたが、k-means法は外れ値の影響を受けやすい特徴があります。
k-means法は、重心をそのクラスタに属するすべてのクラスタとの距離から計算し更新します。
そのため、そのクラスタに外れ値があった場合、外れ値と重心の距離を短くしようと、重心が外れ値の方向に偏ってしまうのです。
k-means法を行う時は、事前に外れ値がないかを散布図で確認し、取り除くことをおすすめします。
k-means法はPythonで簡単に行える
k-means法はPythonを用いることで簡単に行えます。
今回、Pythonのライブラリであるscikit-learn（sklearn）を使うことでk-means法を行います。
ダミーデータの作成からクラスタリングの見える化までを網羅してますので、ぜひ手元にあるデータでk-means法をしてみましょう。
Pythonのコードは以下の通りです。
# 必要なライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
# ダミーデータを生成
# 300個のデータ点
n_samples = 300
# 特徴量は2(変数は2つ)
n_features = 2
# クラスタ数は3とする
n_clusters = 3
# 乱数の生成
X, _ = make_blobs(n_samples=n_samples, n_features=n_features, centers=n_clusters, random_state=0)
# k-means法を定義して学習
kmeans = KMeans(n_clusters=n_clusters, init='random', random_state=0)
kmeans.fit(X)
# クラスタリング結果の見える化
plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_, cmap='viridis', s=50)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], c='red', marker='x', s=200, label='Centroids')
plt.legend()
plt.title('k-means example')
plt.xlabel('feature1')
plt.ylabel('feature2')
plt.show()上記のコードを実行すると、以下のようなクラスタリング結果になります。
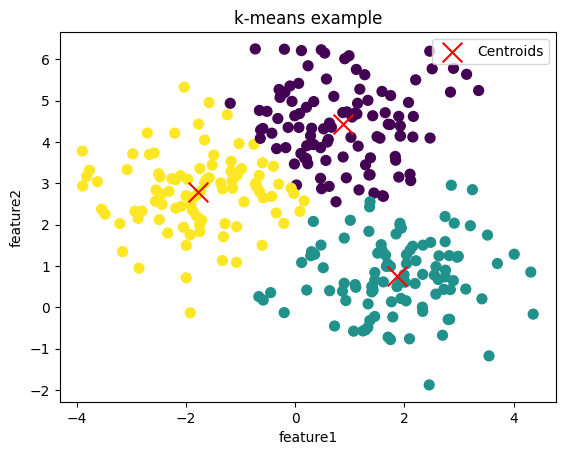
乱数をしているので、同じ結果になればk-means法によるクラスタリングは成功です。
他のデータにも応用してみましょう
まとめ
k-means法はデータのクラスタリングに活用されるアルゴリズムです。
教師なし学習であることから、手元にあるデータをそのまま利用できる特徴があります。
k-means法はクラスタリング手法の一つであることから、さまざまな場面で活用できます。
本記事では代表的な例として以下の3つをご紹介しました。
- 顧客のグループ分け
- 文書や情報の分類
- 社会ネットワークの分析
顧客や情報をグループ分けする需要はどんどん高まっています。
特に、顧客のグループ分けはビジネスに直結します。
そのため、もし自社のデータで顧客分析を行いたい場合は、k-means法を活用することをおすすめします。
k-means法の手順は以下の4ステップです。
- クラスタ数を決定・適当に重心を設定する
- 各データ点で重心との距離を計算し、クラスタに分ける
- 重心点を計算し直す
- 重心点の変動がなくなるまで繰り返す
初期値を設定し、重心を計算し直しながら各データ点が所属するクラスタを確定していくのが主なアルゴリズムです。
機械学習の手法の中でもk-means法は理解しやすい手法であるため、初学者の方でも行いやすいのが特徴になります。
しかし、k-means法には3つの欠点があることも確認しておきましょう。
- クラスタ数を事前に決める必要がある
- 重心の初期値によって結果が変わる
- 外れ値やノイズの影響を受けやすい
クラスタ数に事前に決めるアルゴリズムであるため、最適なクラスタ数が把握できなければ結果が悪くなる可能性があります。
また、重心の初期値の設定をミスすると、極端な結果になってしまうのが注意です。
各データ点との距離で重心を計算するため、外れ値にも影響をされやすいことを把握しておきましょう。
このように欠点は存在しますが、pythonではライブラリを用いて簡単にk-means法を行えます。
記載したコードを参考にk-means法を実行してみましょう。
「機械学習の勉強がなかなか上手く進まない...」
「勉強しても全体像が見えてこない...」
「本当にデータサイエンティストになれるのかな...」
と不安に感じてはいませんか？
僕も勉強しながら同じような悩みを常に持っていました。
ですが、そんな僕の悩みをまるっと解決してくれるサービスをついに見つけました。
データサイエンスを学べるサービスなんて高額でしょ？
データサイエンスを学ぶために高額なお金を払う必要はありません。
僕が利用している『スタアカ』のライトプランは月額980円で動画見放題のコスパ最強サブスクです。
たった月1000円で、もう二度と独学で悩まずに済みます。
正直、「就職・転職までサポートしてほしい」という方にはおすすめできません。
ですが、「勉強の道しるべが欲しい！」「学習を効率的に進めたい」という方にはこの上ないサブスクです。
データサイエンスを学びたい方に最強のサブスク『スタアカ』を気軽に始めてみませんか？
＼月額たった980円！／
講座が毎月追加されるので今後値上がりする可能性大、今が買いどき！
