
- ダイクストラ法って何?
- どんな方法で解いたらいいの?
- Pythonで実装するにはどうするの?
こんな悩みを解決できる記事になっています!
なぜなら、私自身が大学でダイクストラ法を勉強して、分からなかった部分を噛み砕いて説明するためです。
本記事の信頼性
ダイクストラ法は以下のようなステップで最短経路を求める手法になります。
- スタートの頂点から繋がっている辺の距離を確認
- 最短で行ける頂点を選択して、その頂点への最短経路を確定
- これまでの距離の中で最短で行ける頂点を選択
- STEP2とSTEP3を繰り返し、全ての頂点を調べたら終了
この記事を読み終えることで、ダイクストラ法を解けるだけでなく、人に分かりやすく説明できるようになるでしょう。
記事の前半では『ダイクストラ法のアルゴリズム』を紹介し、記事の後半では『ダイクストラ法のPythonでの実装』を具体的に解説します。
「問題の解き方を早く知りたい!」という方は、『ダイクストラ法のアルゴリズム』にジャンプしてください!
月額980円で学べる!

データサイエンスの復習は完ぺきにできていますか?
データサイエンスは勉強する範囲が膨大で、復習に手が回りませんよね。
そんなあなたにおすすめなのが、たった月額980円でサクッと学べる『スタアカ』

数分の動画でビジネスへの活用法も含めて、サクッとデータサイエンスを復習可能。
『何冊も参考書を往復して復習する苦労』とはおさらばです!
サブスクなのでいつでも解約OK。手軽に始めてみませんか?
\月額980円から/
講座が毎月追加されるので今後値上がりする可能性大、今買わなきゃ損するかも!

それでは本編です!
ダイクストラ法とは

ダイクストラ法とはグラフ理論で始点から他の全てのノードへの最短経路を見つけるためのアルゴリズムです。
ダイクストラ法を用いることで、重み付きグラフにおいて、1つのノードから他のノードへの最短距離を効率的に計算できます。
特に、重みが負じゃない場合に用いられ、道路網やインターネットのルーティングなど、多くの分野で応用されています。
地図のようなグラフ上で、1点から他の点への最短経路を見つけるアルゴリズムであると捉えてみましょう。
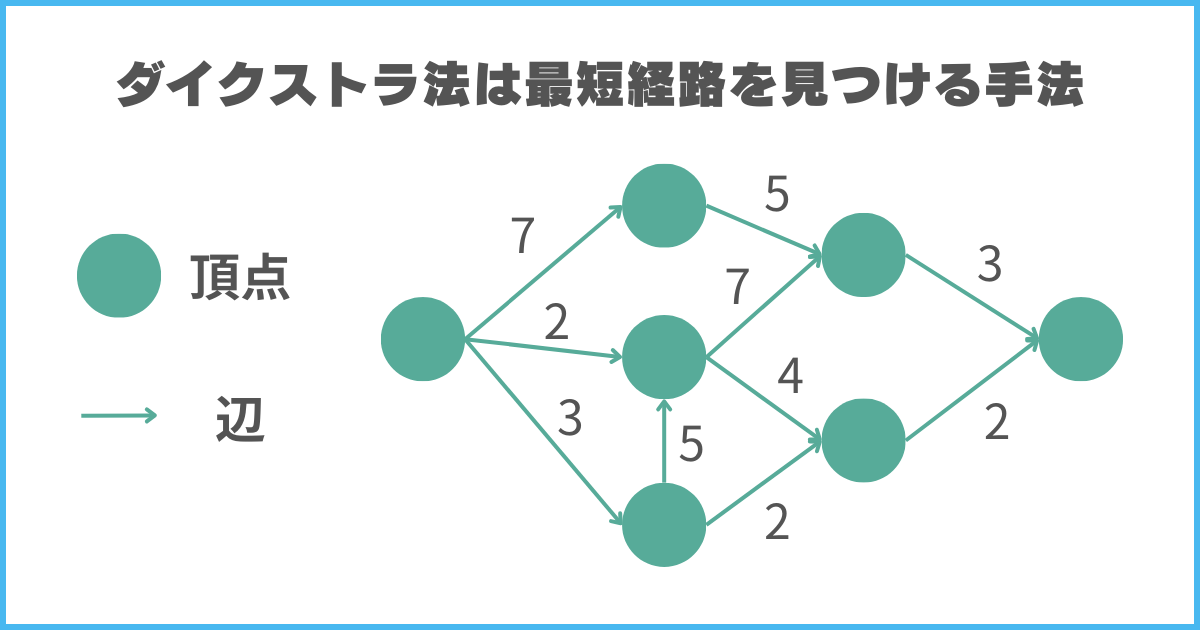
グラフとは、点と点を結ぶ線で構成される図で、ここでいう点は「頂点」、線は「辺」と呼ばれます。
辺には「重み(コスト)」というものがあり、道の長さや時間などの数値を距離として表せるのです。
ダイクストラ法は、この重みが最も少なくなるような経路を計算するアルゴリズムになります。

それではダイクストラ法のアルゴリズムを確認していきましょう
ダイクストラ法のアルゴリズムを例題で解説
この章では、ダイクストラ法のアルゴリズムを解説していきます。
ダイクストラ法のアルゴリズムは大きく4つのステップに分かれていると考えましょう。
- スタートの頂点から繋がっている辺の距離を確認
- 最短で行ける頂点を選択して、その頂点への最短経路を確定
- これまでの距離の中で最短で行ける頂点を選択
- STEP2とSTEP3を繰り返し、全ての頂点を調べたら終了
それぞれのステップについて以下のような例題を用いて説明します。
例題
あなたは自宅から大学まで最短の時間で行けるような経路を探しています。
自宅から大学までに用意されている経路を有向グラフにすると以下のようになりました。
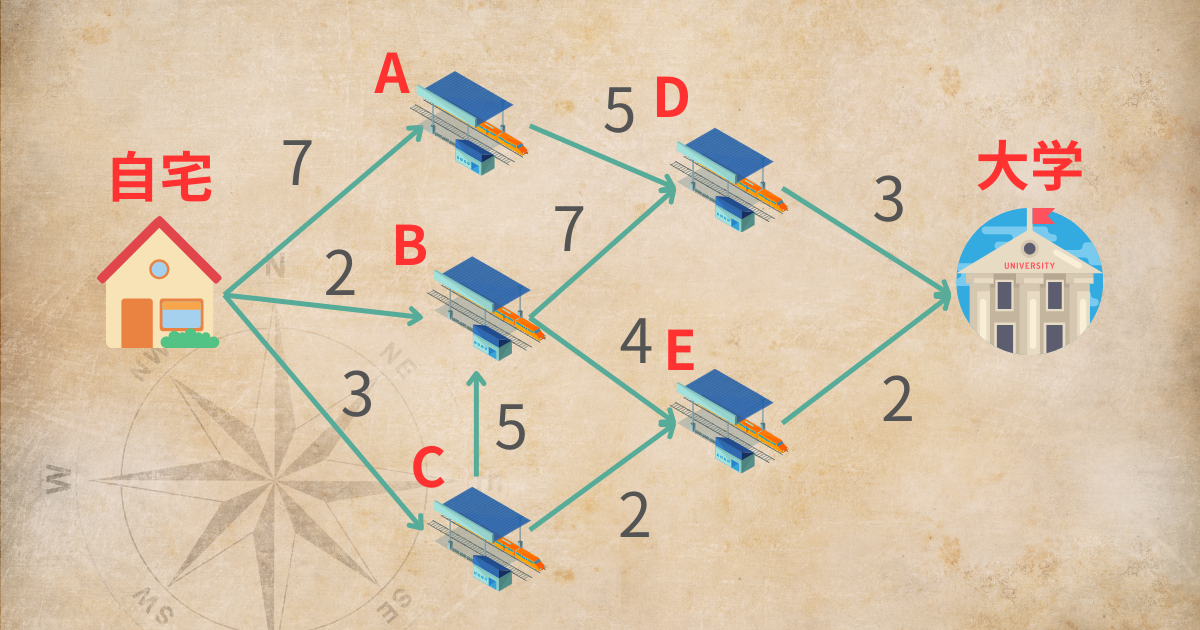
このとき、ダイクストラ法を用いて、最短の時間で行ける経路を求めてください。
今回の例は時間ですが、本来は距離などに対しても用いられるのがダイクストラ法です。
アルゴリズムの説明としては「距離」と記載していますが、実際の問題では自分で時間などに置き換えましょう。
それでは、例題をもとに解説を進めていきます。
STEP1. スタートの頂点から繋がっている辺の距離を確認
まず、スタート地点の頂点から各辺の距離を調べ、隣接する頂点までの距離を確認します。
このとき、スタート地点から直接繋がっている頂点以外の距離は分からないので、∞とすることを覚えておきましょう。
例題だと、自宅からは最寄り駅のA・B・C駅が隣接している頂点となるので、
- A駅まで:7分
- B駅まで:2分
- C駅まで:3分
とそれぞれ時間(距離)を確認しましょう。
そして、大学の最寄り駅のD・E駅はまだ時間が分からないので、∞としておきます。
STEP2. 最短で行ける頂点を選択して、その頂点への最短経路を確定
STEP2では、最短で行ける頂点を選択し、その頂点への最短経路を確定します。
スタート地点から最も距離が短い頂点が見つけられたら、その頂点までの距離を記録して、頂点を調査済みとするのです。
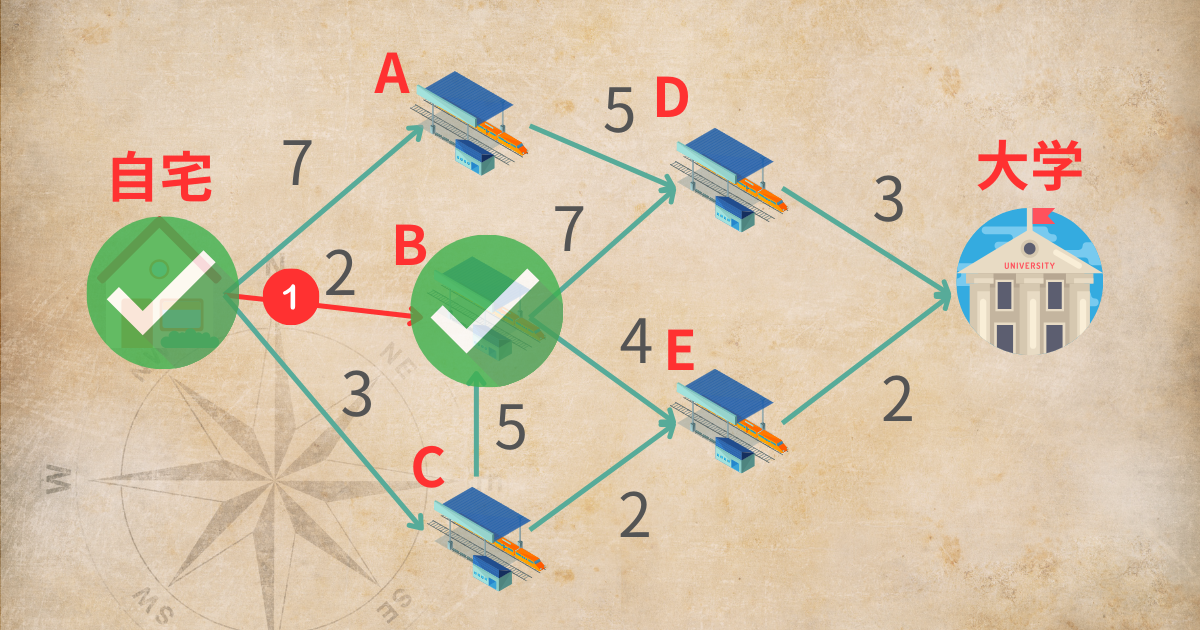
例題では、自宅からだとB駅が最も時間がかからないので、上図のように「B駅までは2分で行ける」と確定させてしまいます。
STEP3では、自宅からB駅までかかった時間も把握しておく必要があるので、B駅まで2分と記録しておきます。
STEP3. これまでの距離の中で最短で行ける頂点を選択
STEP3では、これまでの距離の中で最短で行ける頂点を選択します。
確定した頂点を基に、他の頂点への最短距離を更新していきます。
例題だと、まだ確定していないのは「A・C・D・E・大学」の5つの点で、次に最も早く辿り着ける点を見つけるのです。
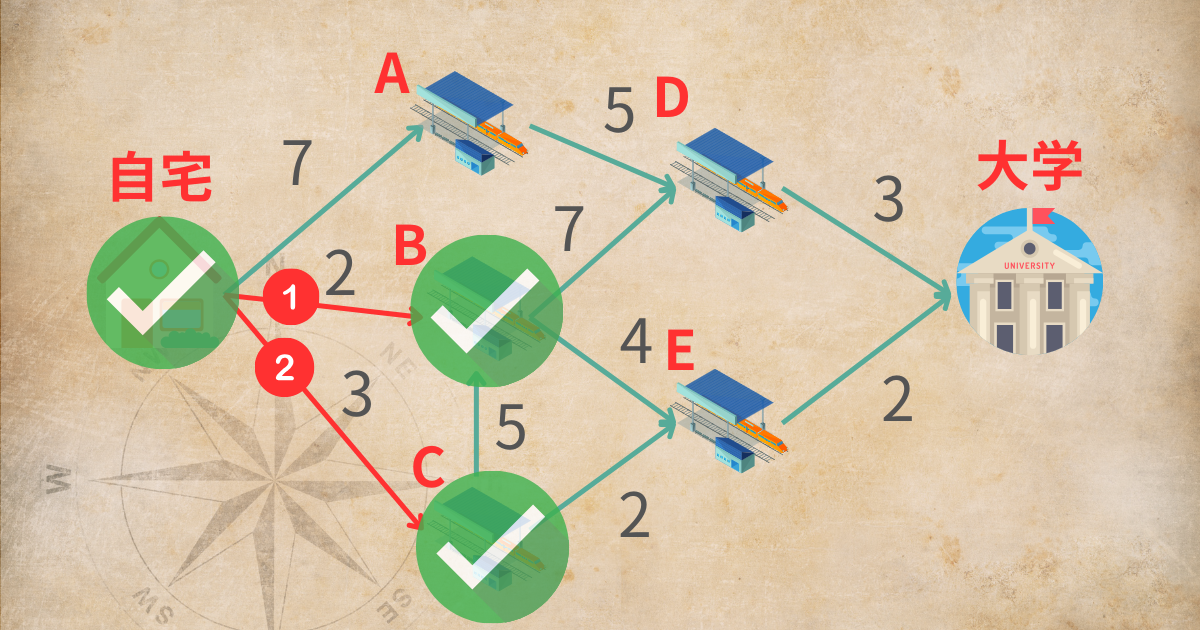
上図のように、次に最短時間となるのは自宅からC駅までだと分かりますね。
そのため、自宅からC駅までが3分であると最短時間を記録しておくのです。
ここまでステップで、B・C駅に辿り着くまでの最短距離を把握できました。
STEP4. STEP2とSTEP3を繰り返し、全ての頂点を調べたら終了
STEP4は、STEP2とSTEP3をすべての頂点を調べ終えるまで繰り返すステップになります。
ここで重要なのは、「ゴールに辿り着いたら」ではなく「すべての頂点を調べ終えたら」ということです。
Pythonで実装するときのアルゴリズムに大きく影響するので、必ず押さえておきましょう。
例題では、最終的に下図のようにすべての頂点を調べられたら完ぺきです!
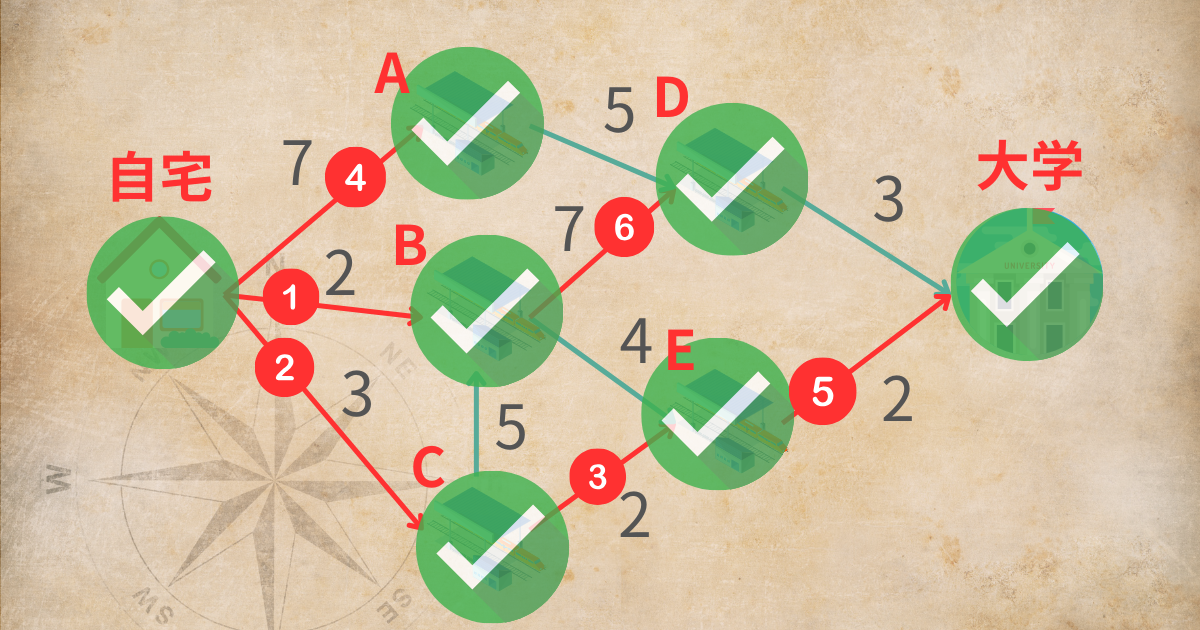
このように、ダイクストラ法を用いることで、
自宅→C駅→E駅→大学
が最短時間で大学に行けるということを導けました。
図では、以下のような経路が最短経路であると分かります。
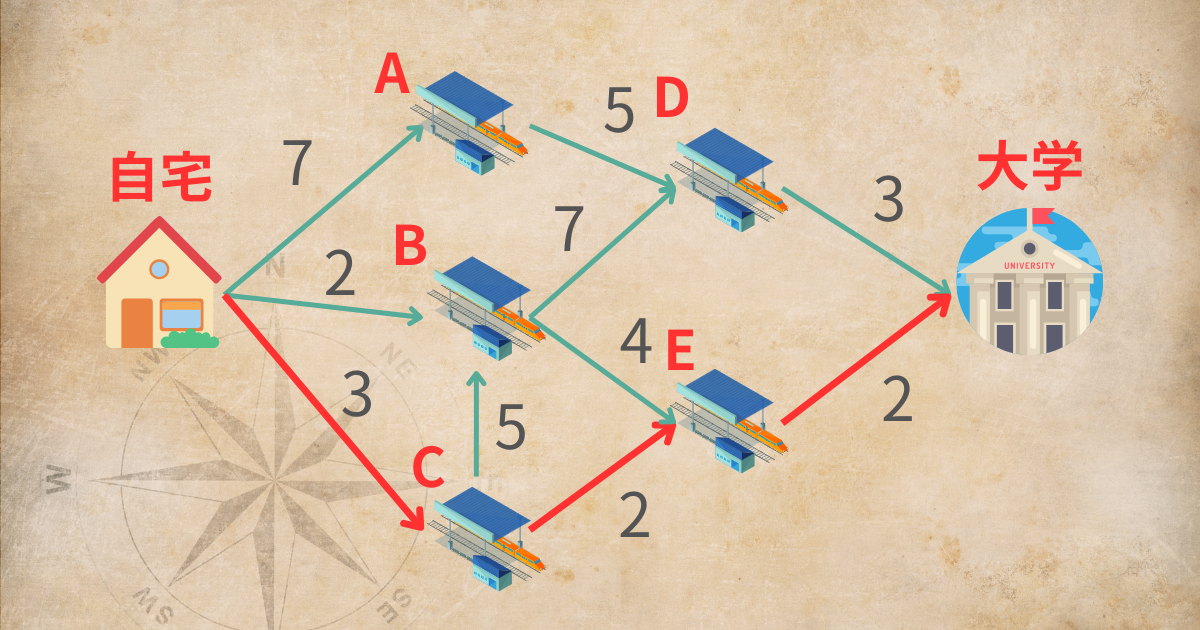
最短経路問題を解きたい場合は、なるべく図にしてみることがおすすめです。
グラフにできたら、ステップを追って1つ1つ確定させましょう。

ここまでの流れを理解するために、もう一度確認しながらやってみてください!
以下では、ダイクストラ法をPythonで実装する方法について解説していきます。
ダイクストラ法をPythonで実装してみる

ダイクストラ法を用いて、始点からグラフ内の他の全ての頂点への最短経路を計算しているのが以下のコードです。
heapqモジュールを使って優先度付きキューを実装し、最短距離が更新されるたびにキューを更新しています。
最終的に、始点から各頂点への最短距離が辞書形式で返されるので実際に実行して確認してみましょう。
import heapq
def dijkstra(graph, start):
# 始点から各頂点への最短距離を格納する辞書
shortest_distances = {vertex: float('infinity') for vertex in graph}
shortest_distances[start] = 0
# 未確定の頂点を管理する優先度付きキュー
priority_queue = [(0, start)]
while priority_queue:
current_distance, current_vertex = heapq.heappop(priority_queue)
# 現在の頂点から隣接する頂点への距離を確認し、必要に応じて更新
for neighbor, weight in graph[current_vertex].items():
distance = current_distance + weight
if distance < shortest_distances[neighbor]:
shortest_distances[neighbor] = distance
heapq.heappush(priority_queue, (distance, neighbor))
return shortest_distances
# グラフの例(各地点間の距離を表す)
graph_example = {
'A': {'B': 1, 'C': 4},
'B': {'A': 1, 'C': 2, 'D': 5},
'C': {'A': 4, 'B': 2, 'D': 1},
'D': {'B': 5, 'C': 1}
}
# アルゴリズムを実行し、最短距離を出力
start_point = 'A'
shortest_paths = dijkstra(graph_example, start_point)
print(shortest_paths)以上のPythonコードでは、ダイクストラ法を使って、地点Aから他の全ての地点への最短距離を計算しています。
ですが、コード内の関数の設定を改良することでゴール地点を定められるので、あなた自身で改良してみてください。
また、実際のグラフが見たい方は以下のPythonコードをコピーして実行しましょう。
import networkx as nx
import matplotlib.pyplot as plt
# 有向グラフの定義
graph_example = {
'A': {'B': 1, 'C': 4},
'B': {'A': 1, 'C': 2, 'D': 5},
'C': {'A': 4, 'B': 2, 'D': 1},
'D': {'B': 5, 'C': 1}
}
# NetworkXのグラフオブジェクトの生成
G = nx.DiGraph()
# ノードとエッジの追加
for node, edges in graph_example.items():
G.add_node(node)
for adjacent, weight in edges.items():
G.add_edge(node, adjacent, weight=weight)
# グラフの描画
pos = nx.spring_layout(G) # ノードの位置をspring layoutアルゴリズムで配置
nx.draw(G, pos, with_labels=True, font_weight='bold') # ノードとエッジの描画
# エッジの重みのラベルを描画
edge_labels = nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)
# 描画の実行
plt.show()
Pythonではnetworkxとmatplotlibというライブラリを使って、有向グラフを簡単に可視化できます。
もし、グラフで可視化したい場合は利用しましょう。
まとめ
ダイクストラ法とはスタート点から他の全てのノードへの最短経路を見つけるためのアルゴリズムです。
最短経路を求める場合は、基本的にダイクストラ法を用いると考えましょう。
ダイクストラ法は4つのステップを意識すると、簡単に最短経路を求められます。
- スタートの頂点から繋がっている辺の距離を確認
- 最短で行ける頂点を選択して、その頂点への最短経路を確定
- これまでの距離の中で最短で行ける頂点を選択
- STEP2とSTEP3を繰り返し、全ての頂点を調べたら終了
まず、問題からグラフを書いて、どのような経路があるのかを把握してください。
そこから、ステップを意識してダイクストラ法を行うと、サクッと求まります。
ダイクストラ法をPythonで実装する方法も解説していますので、一度実行してみることをおすすめします。

ステップを意識して、ダイクストラ法を行いましょう!
あなたはいつもどこかで、
「データサイエンスの勉強がなかなか上手く進まない...」
「勉強しても全体像が見えてこない...」
「本当にデータサイエンティストになれるのかな...」
と不安に感じてはいませんか?
僕も勉強しながら同じような悩みを常に持っていました。
ですが、そんな僕の悩みをまるっと解決してくれたサービスが『スタアカ』です。

データサイエンスを学べるサービスなんて高額なんでしょ?
データサイエンスを学ぶためにもう高額なお金を払う必要はありません。
僕が利用している『スタアカ』のライトプランは月額980円で動画見放題のコスパ最強サブスクです。
「ちょっと興味がある」という方は、受講した感想も載せている記事をご覧ください。
たった月1000円で、もう二度と独学で悩まずに済みます。
正直、「就職・転職までサポートしてほしい」という方にはおすすめできません。
ですが、「勉強の道しるべが欲しい!」「学習を効率的に進めたい」という方にはこの上ないサブスクです。
データサイエンスを学びたい方に最強のサブスク『スタアカ』を気軽に始めてみませんか?
\月額たった980円!/
講座が毎月追加されるので今後値上がりする可能性大、今が買いどき!








